POKOK

TREE




1. 3 definitions of tree :


  1. Tree is a connected undirected graph with no simple circuits (Discrete mathematics And Its Application,  Sixth edition ) 
  2. A diagram that has branches in descending lines showing relationships as of a hierarchy or lineage
  3. A structure for organizing or classifying data in which every item can be traced to a single origin through a unique path. (Forth edition of The American heritage Dictionary, 2009)


2. How to determine a tree?


  1. Tree cannot contains multiple edges or loops 
  2. Tree must be a simple graph.
  3. Tree cannot have a simple circuit.
 Example :


 

3. Rooted tree definitions:

Is a tree in which 1 vertex has been designated as the root and every edge is directed away from the root.

    Characteristic:

A tree together with its roots that produces a directed graph.

   Example:

4. Characteristic/ Properties of tree:





Let T be a graph with n vertices. Then the following statements are equivalent.
  1. T is connected and contains no cycles.
  2. T is connected and has n-1 edges.
  3. T has n-1 edges and contains no cycles.
  4. T is connected and each edge is abridge.
  5. Any two vertices of T are connected by exactly one path.
  6. T contains no cycles, but the addition of any new edge creates exactly one cycles.


5. Application of tree.

  1. binary search tree
  2. decision tree
  3. prefix codes


5.1.Explain how tree are used in modeling.


representing organization

the structure of a large organization can be modeled using a rooted tree. each vertex in this tree represent a position in organization. an edge from one vertex to another indicates that the person represented by the initial vertex is the(direct) boss of the person represented by the terminal vertex

 

6.  Tree Traversal:

Tree Traversal is an ordered root tree often use to store information.

     Types of tree traversal:

1. in order traversal :- visit left most sub tree, visit root, visit other sub-tree left to right.


2. post-order traversal :- visit sub tree left to right, visit root


3. pre-order traversal :- visit root, visit sub tree left to right.





7. Spanning Tree.

Definition: let G be a simple graph. a spanning tree of G is a sub-graph of G that is a tree containing every vertex of  G. 



Theorem 1 :
A simple graph is connected if and only if it has a spanning tree

Application : Spanning Tree Interoperability and  Clustering


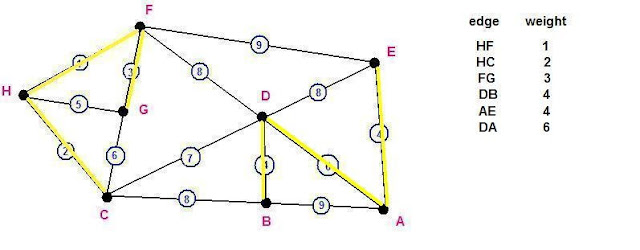
8. Definition of Minimum Spanning Tree

A connected weighted graph is a spanning tree that has smallest possible sum of weight of its edges.

9. The use of Kruskal's Algorithm for finding Minimum Spanning Tree

1. Each vertex is in its own cluster
2. Take the edge e with the smallest weight
         - if e connects two vertices in different clusters,
           then e is added to the MST and the two clusters,
           which are connected by e, are merged into a single cluster
         - if e connects two vertices, which are already in the same
           cluster, ignore it
3. Continue until n-1 edges were selected

Example: 



The shortest edge in the graph is HF which has a weight of 1 so we take that first.






At this point we have two edges that are weight 4, edges DB  and A E.  We can take either one of them first.  It won't matter which.





  1. Now, our next obvious choice to take HG which has a weight of 5.  
  2. However, using this edge would create the cycle HF GH.
  3. Remember, we must avoid cycles.  





Total minimum connecting weight of  27.

  • Komentar /
    • di:
  • / POKOK

    • 0 comments:

    Post a Comment

    Copyright © 2012 group4 book / Template by : Urangkurai